AI 전문가가 되고싶은 사람
(공부용) SHAP: A Unified Approach to Interpreting Model Predictions 본문
(공부용) SHAP: A Unified Approach to Interpreting Model Predictions
Kimseungwoo0407 2024. 8. 30. 01:05SHAP의 배경
대규모 데이터의 활용과 함께 앙상블 모델 및 딥러닝 모델은 높은 예측 정확도를 달성하고 있습니다. 그러나 이러한 모델은 그 구조가 복잡하고 비선형적이기 때문에, 전문가도 모델의 예측 결과를 해석하기 어려운 경우가 많습니다. 이로인해 모델이 왜 정확도가 높은지, 즉 예측의 원인을 이해하는 데 어려움이 발생합니다. 이러한 문제는 모델의 신뢰성을 저하시킬 수 있고, 해석 가능성이 중요한 분야에서 큰 도전 과제가 됩니다. 다양한 해석 방법이 제안되었지만, 특정 상황에서 어떤 방법이 더 적합한지에 대한 기준이 부족합니다.
이 문제를 해결하기 위해 개발된 방법이 바로 SHAP입니다. SHAP은 모델이 어떤 특성(feature)에 얼마나 의존해서 예측을 했는지를 정량적으로 보여줍니다. 이를 통해 각각의 특성이 예측 결과에 얼마나 중요한지 알 수 있습니다. SHAP은 가법적 특성 중요도 측정 방법을 기반으로 새로운 접근 방식을 제시합니다.
SHAP의 기본 개념
게임 이론의 Shapley 값을 기반으로 하여, 각 특성이 모델의 예측에 미치는 영향을 정량화하는 것입니다.
Shapley 값은 게임 이론에서 각 플레이어가 공동의 성과에 기여한 정도를 측정하는 방법으로 각 특성의 기여도를 공정하게 분배하기 위해, 모든 가능한 특성 조합에 대해 그 특성이 포함된 경우와 포함되지 않은 경우의 예측 차이를 계산합니다. 다시 말해, 각 특성이 모델의 예측에 기여한 정도를 측정하는 방법입니다.
또한 SHAP은 "Additive"라는 특성을 가지고 있는데 SHAP 값이 각 특성의 기여도를 합산하여 최종 예측을 생성한다는 의미입니다. 이 말은 모델의 예측은 기본값(모든 특성이 0일 때의 예측)과 각 특성의 SHAP 값을 합산하여 계산됩니다.
SHAP 값 계산
SHAP 값 계산의 시작점은 기본값입니다. 이는 모든 특성이 무시된 상태에서 모델이 예측하는 값으로, 일반적으로 훈련 데이터의 평균 예측값으로 설정됩니다. 예를 들어, 주택 가격을 예측하는 모델에서 기본값이 300,000달러라고 가정했을 때, 이 값은 모든 특성(예: 면적, 위치, 연식 등)을 고려하지 않고, 단순히 모델이 모든 주택 데이터에서 예측한 평균 주택 가격을 의미합니다.
\[ \varphi_i = \sum_{S \subseteq N \setminus \{i\}} \frac{|S|!(|N| - |S| - 1)!}{|N|!} \left( v(S \cup \{i\}) - v(S) \right) \]
여기서 는 특성 의 SHAP 값, N은 모든 특성의 집합, S는 특성의 부분 집합, v(S)는 집합 S의 예측값을 나타냅니다. 이 식은 모든 가능한 특성 조합에 대해 특성 i가 추가되었을 때의 기여도를 계산합니다.
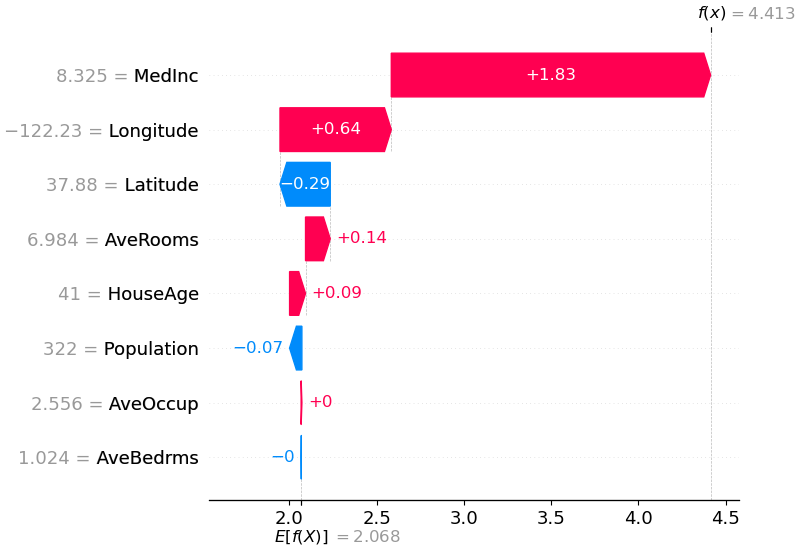
SHAP 값은 각 특성이 모델 예측에 미치는 영향을 정량화하여, 사용자가 각 특성이 예측에 어떻게 기여하는지를 이해할 수 있게 해줍니다. 예를 들어, 특정 특성의 SHAP 값이 양수인 경우, 해당 특성이 예측을 증가시키는 방향으로 기여하고 있다는 것이고, 반대로 SHAP 값이 음수인 경우, 해당 특성이 예측을 감소시키는 방향으로 기여하고 있음을 나타냅니다.

해석 가능성의 이점
SHAP 값은 모든 특성에 대해 일관된 기여도를 제공하므로, 사용자가 모델의 예측을 이해하고 신뢰하는 데 도움을 줍니다. 이는 복잡한 모델에서 매우 중요한 요소입니다. Shapley 값의 특성 덕분에, SHAP은 각 특성이 예측에 기여한 정도를 공정하게 분배합니다. 이는 모델 해석의 신뢰성을 높이는 데 기여합니다. 또한 SHAP은 특성 간의 상호작용을 고려할 수 있는 방법을 제공하여, 복잡한 모델의 예측을 더 깊이 이해할 수 있게 돕습니다.
기존 해석 방법과의 비교
SHAP, LIME, DeepLIFT는 모두 복잡한 모델의 예측을 해석하기 위해 개발된 방법들로, 서로 다른 방식으로 특성의 기여도를 평가하므로 비교해보겠습니다.
● LIME
- 장점
특정 예측에 대한 로컬 해석을 제공하며, 복잡한 모델을 단순한 선형 모델로 근사하여 해석합니다.
사용자가 이해하기 쉬운 형태로 결과를 제공합니다.
- 단점
LIME의 결과는 샘플링에 의존하므로, 샘플링의 질에 따라 해석의 일관성이 떨어질 수 있습니다.
특성 간의 상호작용을 고려하지 않기 때문에, 복잡한 관계를 설명하는 데 한계가 있습니다.
● DeepLIFT
- 장점
DeepLIFT는 신경망의 내부 구조를 활용하여 각 특성의 기여도를 계산합니다.
이는 신경망의 특정 레이어에서의 기여도를 명확히 설명할 수 있습니다.
계산 속도가 빠르며, 대규모 신경망에 적합합니다.
- 단점
특정 구조(신경망)에 최적화되어 있어, 다른 유형의 모델에 적용하기 어렵습니다.
SHAP과 비교할 때, 특성 간의 상호작용을 완벽하게 반영하지 못할 수 있습니다.
● SHAP
- 장점
게임 이론에 기반하여 각 특성의 기여도를 공정하게 분배한다 -> 특성 기여도의 일관성과 공정성을 보장합니다.
SHAP 값은 모든 가능한 특성 조합을 고려하여 계산되므로, 특성 간의 상호작용을 자연스럽게 반영합니다.
다양한 모델에 적용 가능하고 모든 모델에 대해 동일한 해석 기준을 제공하므로, 다양한 모델 간의 비교가 용이합니다.
- 단점
SHAP 값 계산은 계산 비용이 높고, 대규모 데이터셋에서 시간이 많이 소요될 수 있습니다.
SHAP의 응용 사례
● 의료 분야
심장병 예측 모델에서 SHAP을 사용하여 나이, 혈압, 콜레스테롤 수치와 같은 특성이 환자의 위험 점수에 미치는 영향을 분석합니다.
● 금융 분야
대출 신청자의 신용 점수를 예측하는 모델에서 SHAP 값을 사용하여 각 특성이 대출 승인 여부에 미치는 영향을 분석합니다.
● 마케팅 분야
마케팅에서는 고객 행동 예측 모델에서 SHAP을 활용하여 고객의 구매 결정에 영향을 미치는 요인을 분석 합니다.
● 제조 및 품질 관리
제품 결함 예측 모델에서 SHAP을 사용하여 원자재 품질, 생산 공정 변수, 작업자 경험 등이 결함 발생에 미치는 영향을 분석합니다.
● 자율주행차
자율주행차의 경로 선택 모델에서 SHAP을 사용하여 도로 상황, 교통 신호, 주변 차량의 위치 등이 경로 결정에 미치는 여향을 분석합니다.
SHAP의 결론 및 향후 연구 방향
SHAP는 복잡한 모델의 예측을 해석하는 데 중요한 역할을 하며, 기존의 여러 방법을 통합하여 바람직한 속성을 가진 유일한 솔루션을 제공합니다. 향후 연구는 모델 유형별 SHAP 값 추정 방법 개발, 상호작용 효과 추정 통합, 새로운 설명 모델 클래스 정의에 중점을 두어야 합니다. SHAP은 모델 해석 분야에서 지속적으로 중요한 기여를 할 것으로 기대되며, 사용자 신뢰를 구축하고 모델 개선에 대한 통찰을 제공하는 데 필수적인 도구로 자리잡을 것입니다.
'논문' 카테고리의 다른 글
| (공부용) VERY DEEP CONVOLUTIONAL NETWORKSFOR LARGE-SCALE IMAGE RECOGNITION (2) | 2024.09.07 |
|---|---|
| (구현) Going deeper with convolutions (3) | 2024.09.06 |
| (공부용) Going deeper with convolutions (0) | 2024.09.06 |
| (구현) ImageNet Classification with Deep Convolutional Neural Networks (PyTorch) (1) | 2024.09.04 |
| (공부용) ImageNet Classification with Deep Convolutional Neural Networks (4) | 2024.09.03 |





