AI 전문가가 되고싶은 사람
가설 검정, 중심 극한 정리, t-test 정리 및 복습 본문
● 가설과 가설 검정 이야기
1. 모집단(Population)과 표본(Sample)
○ 모집단 : 우리가 알고 싶은 대상 전체 영역 ( 데이터 )
○ 표본 : 그 대상의 일부 영역 ( 데이터 )
* 모집단에서 표본을 뽑음으로써 일부분으로 전체를 추정하고자 함
2. 비즈니스 이해 단계에서 사용
○ 비즈니스 문제로부터 우리의 관심사(Y)를 도출 -> Y에 영향을 주는 요인(X)들을 뽑아서 가설 수립
ex) 고객 이탈 예측(y)에 영향을 주는 요인(x)는?
고객의 가입기간(x1) -> 이탈여부(y)
성별(x2) -> 이탈여부(y)
직업(x3) -> 이탈여부(y)
3. 귀무가설(H0), 대립가설(H1)
○ 귀무가설 ( 영가설, 현재의 가설, 보수적인 입장 ) : 현재 주장되고 있는 가설
ex 1) 매장지역에 따라 수요량에 차이가 없다.
ex 2)비가 온 날에는 항상 개구리를 본다.
○ 대립가설 ( 연구가설, 새로운 가설, 내가 바라는 바 ) : 귀무 가설이 맞지 않고 틀리다는 증거를 찾아내기 위한 가설
ex 1) 매장지역에 따라 수요량에 차이가 있다.
ex 2) 비가 온 날에도 개구리를 보지 못하는 경우가 있다.
4. 모집단에서 추출한 표본으로부터 대립가설을 확인하고, 모집단에서도 맞을 것이라 주장
○ 분포 + 판단 기준 필요 ( p-value : 유의수준이라고 부르며, 0.05 (5%) 혹은 좀 더 보수적인 기준으로 0.01(1%)를 사용
○ 0.05 혹은 0.01 보다는 p-value가 작아야, 차이가 있다고 판단
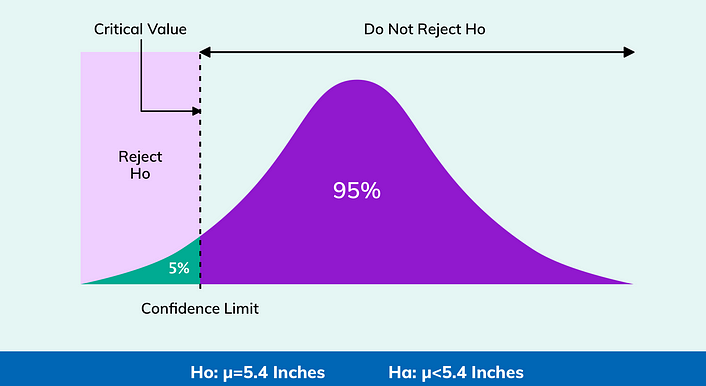
5. 인도 여성의 평균 키가 5.4 인치 미만 -> 단측 검정
○ H0 ( 귀무가설 ) : 평균 높이 (u) = 5.4 인치
○ H1 ( 대립가설 ) : 평균 높이 (u) < 5.4 인치
왼쪽 꼬리 분포
5-1. 인도 여성의 평균 키가 5.4 인치 이상 -> 단측 검정
○ H0 ( 귀무가설 ) : 평균 높이 (u) = 5.4 인치
○ H1 ( 대립가설 ) : 평균 높이 (u) >= 5.4 인치
오른쪽 꼬리 분포

6. 양측 가설 검정 ( 인도 여성의 평균 키는 5.4 인치 )
○ H0 ( 귀무가설 ) : 평균 키 (u) = 5.4 인치
○ H1 ( 대립가설 ) : 평균 키 (u) =! 5.4 인치
양측

7. 상관 계수
○ 값의 범위 : -1 ~ 1
○ -1 혹은 1에 가까울 수록 강한 상관관계, 반대로 0에 가까울 수록 약한 상관관계
○ p-value : 0.05보다 작으면 상관관계가 있다고 판단

8. 우리가 사용할 도구
○ 연속형 (x) - 연속형 (y) : ( 시각화 - scatter (산점도) , 수치화 - 상관분석 )
○ 연속형 (x) - 범주형 (y) : ( 시각화 - Boxplot, Histogram, Density plot )
8-1. 연속형 (x) - 연속형 (y)
○ 해당 carseats 데이터를 사용해서 설명

○ Scatter plot ( Price -> Sales )
sns.scatterplot(x='Price', y = 'Sales', data = data)
plt.show()
result = spst.pearsonr(data['Price'], data['Sales'])
print(f'상관계수 : {result[0]}, p-value : {result[1]}')
8-2. 범주형(x) - 연속형(y)
○ titanic 데이터를 사용해서 설명

○ 시각화 - 평균 비교 ( barplot )
- 두 변수간의 차이가 애매!
- 눈으로 판단하기 힘

○ 수치화 - t-test
* 주의사항 - 데이터에서 NaN이 있으면 계산이 안됨, notnull() 등으로 NaN을 제외한 데이터 사용해야 함
- 여기서 t 통계량이란 두 평균의 차이를 표준오차로 나눈 값으로 두 평균의 차이로 이해해도 됨
- 보통, t 값이 -2보다 적거나, 2보다 크면 차이가 있다고 봄
1) 데이터 준비
# 먼저 NaN이 있는지 확인해 봅시다.
titanic.isna().sum()
# NaN 행 제외
temp = titanic.loc[titanic['Age'].notnull()]
# 두 그룹으로 데이터 저장
died = temp.loc[temp['Survived']==0, 'Age']
survived = temp.loc[temp['Survived']==1, 'Age']
2) t-test
spst.ttest_ind(died, survived)
- t 값이 2보다 크고, p-value가 0.05보다 작기 때문에 귀무가설을 기각하고 대립가설을 채택한다 -> 두 평균의 차이가 있다!
9. 중심 극한 정리 ( 큰 규모의 표본에서 특히 중요한 역할을 함 )
○ 어떤 모집단에서 표본을 여러 번 추출하면, 그 표본 평균들의 분포가 정규분포를 따르게 된다
○ 중요한 부분! : 원래의 모집단의 분포 형태에 상관없이 성립
ex) 우리가 전 세계의 모든 성인 남성의 키를 알고 싶다고 가정했을 때, 이것은 거의 불가능한 일이다
but 중심 극한 정리를 이용한다면 이 문제를 해결할 수 있음!
대상 집단에서 일부를 무작위로 선택(표본추출)하고, 그들의 키의 평균을 계산
-> 각 표본의 평균들이 이루는 분포는 정규분포를 따르게 됨
-> 해당 정규분포의 평균과 표준편차를 이용하면 전체 모집단의 키에 대한 유용한 정보를 얻을 수 있음

'기자단 활동' 카테고리의 다른 글
| 웹 크롤링 - 1일 (1) | 2024.03.07 |
|---|---|
| 분산 분석 ( ANOVA) 및 이변량 분석 복습 (0) | 2024.03.01 |
| 파이썬 시각화와 단변량 분석 복습 ( + 시계열 데이터 처리 ) (1) | 2024.02.28 |
| 파이썬 프로그래밍 ( 데이터 프레임 변경 및 결합 ) 복습 (1) | 2024.02.26 |
| 파이썬 프로그래밍 (pandas) 복습 (0) | 2024.02.24 |




