AI 전문가가 되고싶은 사람
RNN 구현 본문
https://www.youtube.com/watch?v=cdGBloT9vDk
훈민정음 문장을 학습시키고 한 구절을 입력했을 때, 이후의 출력을 뽑아내는 바닐라 RNN을 실습해보았다.
RNN 구현 순서
1. 데이터 전처리
2. 가중치 초기화
3. 순전파
4. 역전파
5. 예측
6. 학습 루프
데이터 전처리
사용 문장
나라의 말이 중국과 달라 문자와 서로 통하지 아니하니, 이런 까닭으로 어리석은 백성이 이르고자 할 바가 있어도 마침내 제 뜻을 능히 펴지 못할 사람이 많다. 내가 이를 위하여 가엾이 여겨 새로 스물여덟 자를 만드노니 사람마다 하여금 쉬이 익혀 날마다 쓰는 데 편하게 하고자 할 따름이다.
def data_preprocessing(data):
data = re.sub('[^가-힣]', ' ', data) # 한글 이외의 문자 제거
tokens = data.split() # 단어 단위로 분리
vocab = list(set(tokens)) # 고유 단어 집합
vocab_size = len(vocab) # 단어 집합의 크기
word_to_ix = {word: i for i, word in enumerate(vocab)} # 단어 -> 인덱스
ix_to_word = {i: word for i, word in enumerate(vocab)} # 인덱스 -> 단어
return tokens, vocab_size, word_to_ix, ix_to_word먼저 tokens는 단순히 띄어쓰기를 기준으로 단어를 분리하여 사용하였다.

vocab_size는 tokens에서 중복을 제거한 후 len 함수를 통해 개수를 세었다.

해당 RNN 실습 코드에서 word_to_ix는 각 단어를 고유한 정수 인덱스로 변환한 것이고, ix_to_word는 정수 인덱스를 원래 단어로 변환한 것이다.


가중치 초기화

def init_weights(h_size, vocab_size):
U = np.random.randn(h_size, vocab_size) * 0.01 # 입력 -> 은닉층
W = np.random.randn(h_size, h_size) * 0.01 # 은닉 -> 은닉
V = np.random.randn(vocab_size, h_size) * 0.01 # 은닉 -> 출력
return U, W, V가중치 초기화 함수는 U,W,V를 임의의 값으로 두게 한다.
U : 입력 벡터에서 은닉 상태로의 가중치
W : 이전 은닉 상태에서 현재 은닉 상태로의 가중치
V : 은닉 상태에서 출력으로의 가중치
순전파
순전파 과정은 입력 -> 은닉층 -> 출력층으로 신호를 전달하여 예측값을 계산하고, 이를 통해 손실(loss)을 계산하는 과정이다.
def feedforward(inputs, targets, hprev):
loss = 0 # 총 손실을 저장하는 변수, 모든 시점의 손실을 누적한다.
xs, hs, ps, ys = {}, {}, {}, {}
hs[-1] = np.copy(hprev)
for i in range(seq_len):
xs[i] = np.zeros((vocab_size, 1))
xs[i][inputs[i]] = 1 # 입력 단어의 원핫 인코딩
hs[i] = np.tanh(np.dot(U, xs[i]) + np.dot(W, hs[i - 1])) # 은닉 상태
ys[i] = np.dot(V, hs[i]) # 출력 벡터
ps[i] = np.exp(ys[i]) / np.sum(np.exp(ys[i])) # 소프트맥스 확률
loss += -np.log(ps[i][targets[i], 0]) # 손실 계산 (크로스 엔트로피)
return loss, ps, hs, xsxs,hs,ps,ys 는 각 시점 t의 입력, 은닉상태, 출력 확률, 로그잇값을 저장하는 딕셔너리다.
hs[-1]은 이전 시점의 은닉 상태 초기화. ht-1을 저장하여 첫 시점 계산에 사용한다.
for i in range(seq_len):
xs[i] = np.zeros((vocab_size, 1))
xs[i][inputs[i]] = 1 # 입력 단어의 원핫 인코딩해당 부분이 입력 단어의 원핫 인코딩을 해준다고 하는데 간단히 이해하기 위해 예시를 들어보겠다. 다음과 같이 np.zeros((5,1))을 할 경우 5개의 행이 생기게 되고 이는 모두 0으로 초기화된 상태이다.
np.zeros((5, 1))
[[0.]
[0.]
[0.]
[0.]
[0.]]이제 xs[i] = np.zeros((vocab_size, 1)) 해당 부분을 살펴보면 xs[i]에 vocab_size가 현재 43이므로 43개의 행을 가진 리스트를 생성하는것이고, 이후 xs[i][inputs[i]] = 1이라는 부분을 통해 inputs으로 들어온 값의 i 부분만 1로 하여라고 하는 것이다.
xs[i][5] = 1위 예시를 들어보자면, 아래와 같게 된다.
[[0.]
[0.]
[0.]
[0.]
[0.]
[1.] # 5번째 인덱스가 1
[0.]
.
.
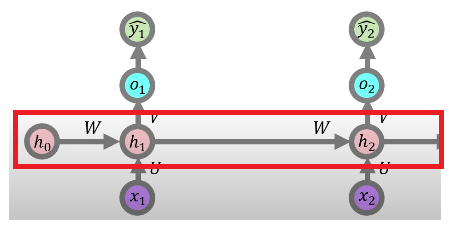
[0.]]다음 코드는 hs[i] = np.tanh(np.dot(U, xs[i]) + np.dot(W, hs[i - 1])) 이다. 해당 부분은 아래 그림을 통해 이해를 해보겠다.

RNN은 이전의 은닉층과 현재 입력을 결합하여 새로운 은닉측을 계산한다. 이 과정은 다음의 수식을 사용한다.
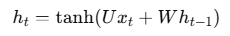
이전 은닉층 h0에 가중치 W를 곱한다. 이는 이전의 은닉 정보를 현재 시점으로 전달하기 위한 과정이다. 이후 현재 입력 x1에 가중치 U를 곱한다. 이는 입력 데이터가 은닉층에 얼마나 영향을 미칠지 결정한다. 두 결과를 더한 후 tanh 활성화 함수를 적용한다. 위 이미지에 대한 계산식은 아래와 같다.
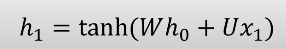
왜 tanh를 적용할까?
선형 함수의 경우 여러 층을 쌓아도 최종적으로 하나의 선형 함수로 단순화 된다. 즉 여러 층을 쌓아도 여전히 선형 관계를 유지하며, 학습할 수 있는 표현력이 제한된다.
ex) f(x) = ax+b
f(f(x)) = a(ax+b) + b = a^2x + ab + b
만약, 비선형 함수를 도입하면 층을 쌓을수록 비선형이 누적되므로 더 복잡한 관계를 표현할 수 있다. 간단히 선형은 직선 관계로 표현하려다보니 불가한 일을 곡선 형태의 복잡한 관계를 학습할 수 있도록 해준다고 생각하면 된다. 해당 내용도 추후에 다루면 좋을 것 같다.
다음으로 아래와 같은 순서를 거치게 되는데, ys[i]는 작성한 그대로 V와 hs[i]를 통해 o1을 만드는 과정이다.
ys[i] = np.dot(V, hs[i]) # 출력 벡터
ps[i] = np.exp(ys[i]) / np.sum(np.exp(ys[i])) # 소프트맥스 확률
loss += -np.log(ps[i][targets[i], 0]) # 손실 계산 (크로스 엔트로피)이후 ps[i]는 소프트맥스 함수를 활용해 각 단어가 다음 단어로 등장할 확률을 나타낸다.
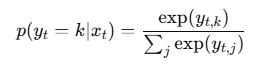
마지막으로 loss에서 ps[i][targets[i], 0 부분은 정답 단어의 확률을 의미하고, 그 로그값에 음수를 취해 누적 손실을 계산한다.
예시로 ps[i]가 [0.1,0.7,0.2]라고 하면 정답 단어는 targets[i] = 1(2번째 단어)이 된다.
따라서 ps[i][1] = 0.7이다. log(0.7) = - 0.3567이 되고 크로스 엔트로피 손실은 음수 값을 취하므로 0.3567이 된다. 해당 방식으로 구한 손실 값들을 loss에 누적으로 더해준다는 의미이다.
역전파
def backward(ps, hs, xs):
dV = np.zeros(V.shape)
dW = np.zeros(W.shape)
dU = np.zeros(U.shape)
for i in range(seq_len)[::-1]: # 역순으로 역전파
output = np.zeros((vocab_size, 1))
output[targets[i]] = 1
ps[i] = ps[i] - output
dV += ps[i] @ hs[i].T # dL/dV
delta_recent = (V.T @ ps[i]) * (1 - hs[i] ** 2) # dL/dh
for j in range(i + 1)[::-1]:
dW += delta_recent @ hs[j - 1].T # dL/dW
dU += delta_recent @ xs[j].T # dL/dU
delta_recent = (W.T @ delta_recent) * (1 - hs[j - 1] ** 2)
return dU, dW, dV, hs[len(inputs) - 1]dV, dW, dU는 각각 출력층, 은닉층-은닉층 가중치, 입력층-은닉층 가중치에 대한 기울기를 저장할 변수들이다.
np.zeros(V.shape)는 각 가중치 행렬의 크기와 같은 형태의 0으로 초기화된 배열을 생성한다.
for i in range(seq_len)[::-1]: # 역순으로 역전파시퀀스의 마지막에서부터 시작해서 첫 번째까지 진행되므로, 해당 부분을 통해 역전파한다는 것을 알 수 있다.
output = np.zeros((vocab_size, 1))
output[targets[i]] = 1
ps[i] = ps[i] - outputoutput은 각 시간 스텝에서의 실제 정답을 나타낸다. targets[i]는 해당 시점의 실제 단어를 1로 설정하고 나머지는 0으로 설정한다.
ps[i]는 모델이 예측한 확률 분포이다. ps[i] - output은 예측값과 실제값의 차이를 계산한 것이며, 이는 크로스 엔트로피 손실의 기울기입니다. 이 값을 ps[i]에 저장하여 다음 단계로 전파한다.
예시를 들자면, vocab = ["봄", "여름", "가을", "겨울"]이 있고, targets[i] = 2이면 실제 정답은 가을이 된다. 이제 output 벡터는 targets[i] = 2에 해당하는 인덱스를 1로 설정하고 나머지 인덱스는 0으로 설정한다. 즉
output = [[0],[0],[1],[0]]이 된다. 이후 확률 분포를 다음과 같이 가정하고, ps[i] = [[0.1],[0.2],[0.5],[0.2]]
ps[i] - output을 계산하면 [[0.1],[0.2],[-0.5],[0.2]]가 되고 해당 값이 오차가 된다.
이후의 목적은 오차를 최소화하는 것으로 ps[i]값과 실제 정답 output 사이의 차이를 최소화하려는 방향으로 학습을 진행한다.
dV += ps[i] @ hs[i].T # dL/dVps[i]는 예측된 확률 분포이고, hs[i]는 해당 시점에서의 은닉 상태이다.
ps[i] @ hs[i].T는 V에 대한 기울기로 V는 은닉층에서 출력층으로의 가중치이다.
이 값은 예측된 확률 분포와 은닉 상태의 전치 행렬을 곱한 값이다.
이렇게 계산된 기울기를 dV에 누적하여 저장한다.
ps[i] = np.array([[0.1], [0.2], [0.5], [0.2]])예측 확률이 다음과 같고, 차원이 3인 은닉층이 아래와 같다면 ps[i]는 4x1 벡터이고, hs[i]는 3x1 벡터가 된다.
hs[i] = np.array([[0.7], [0.3], [-0.4]])기존 계산식과 같이 은닉 벡터를 전치하게 되면 4x1 @ 1x3이 되므로 4x3 행렬이 된다. 계산한 값을 dV에 누적하여 가중치 업데이트를 진행한다.
다음으로 현재 시점에서의 은닉 상태의 기울기를 계산하는 과정이다.
delta_recent = (V.T @ ps[i]) * (1 - hs[i] ** 2)ps[i]는 현재 시점에서 모델이 예측한 출력 확률 분포이고 vocab_size x 1 형태의 벡터이다. 실제로 모델이 예측한 각 단어의 확률을 나타낸다. V는 은닉층에서 출력층으로의 가중치 행렬로 V의 크기는 output_size x hidden_size이다.
V.T @ ps[i]는 출력층에서의 오류를 은닉층에 전파하는 과정으로, 출력층에서 발생한 오차가 은닉층에 어떻게 영향을 미치는지 계산하는 것이다. ps[i]는 vocab_size x 1이고, V.T는 hidden_size x vocab_size이므로 곱셈 결과는 hidden_size x 1 크기의 벡터가 된다. 이 벡터는 현재 은닉 상태에 대한 오류를 나타낸다.
hs[i]는 현재 시점에서의 은닉 상태이고, hidden_size x 1 형태로, tanh 함수로 활성화된 값이다. tanh 함수의 미분은 1 - tanh(x)^2이기에 은닉 상태가 hs[i]로 주어졌을 때, 이 값은 1 - hs[i]^2로 계산된다. 이 값은 은닉 상태의 기울기를 계산할 때 사용된다. 왜냐하면 역전파에서 은닉층의 오류를 전파할 때, 활성화 함수의 미분값을 곱해줘야 하기 때문이다. tanh 함수는 비선형 함수이기 때문에 미분이 필요하다.
즉, delta_recent는 현재 시점의 은닉 상태에 대한 기울기이며, 이는 역전파에서 중요한 역할을 합니다. 이 값은 이전 시점으로 전달되는 은닉 상태의 기울기가 됩니다. 즉, 이 기울기를 이용해 W, U 등의 가중치에 대한 기울기를 계산할 수 있습니다.
해당 부분은 RNN에서 가중치를 업데이트하기 위한 기울기 계산 과정이다.
for j in range(i + 1)[::-1]:
dW += delta_recent @ hs[j - 1].T # dL/dW
dU += delta_recent @ xs[j].T # dL/dU
delta_recent = (W.T @ delta_recent) * (1 - hs[j - 1] ** 2)delta_recent는 은닉층의 기울기를 의미하고, hs[j - 1].T는 이전 시간 스텝의 은닉 상태의 전치 행렬이다.
delta_recent @ hs[j - 1].T는 은닉층과 은닉층 사이의 가중치에 대한 기울기를 계산한다. 이 곱셈은 은닉 상태의 기울기(delta_recent)와 이전 은닉 상태(hs[j - 1])의 관계를 나타내며, 그 기울기를 계산하여 dW에 더한다.
xs[j]는 현재 시점의 입력값이다.
delta_recent @ xs[j].T는 입력층과 은닉층 사이의 가중치에 대한 기울기(dL/dU)를 계산한다. 이 연산은 은닉 상태의 기울기(delta_recent)와 현재 입력값(xs[j])을 곱하여 dU에 더한다.
delta_recent = (W.T @ delta_recent) * (1 - hs[j - 1] ** 2)
이 부분은 다음 시간 스텝으로 전파될 기울기를 계산하는 과정이다.
W.T는 은닉층-은닉층 가중치의 전치행렬이며, 이 연산은 현재 은닉 상태에서의 기울기를 이전 은닉 상태로 전달한다.
hs[j - 1]은 tanh 함수에 의해 변형되었기 때문에, 이를 미분하여 기울기를 조정해야 한다.
이 두 값을 곱한 결과가 delta_recent에 할당되며, 이는 이전 시간 스텝으로 전파될 은닉 상태의 기울기이다. 이 기울기는 다음 반복에서 dW와 dU 계산에 사용되며, 은닉층-은닉층과 입력층-은닉층 가중치에 대한 기울기를 계속해서 누적시킨다.
예측
예측 부분은 주석으로 설명하였습니다.
def predict(word, length):
# 입력 단어 원-핫 벳터로 변환
x = np.zeros((vocab_size, 1))
x[word_to_ix[word]] = 1
ixes = []
# 초기 은닉 상태 설정
h = np.zeros((h_size, 1))
for t in range(length):
h = np.tanh(np.dot(U, x) + np.dot(W, h)) # 은닉 상태 갱신
y = np.dot(V, h) # 출력층
p = np.exp(y) / np.sum(np.exp(y)) # 소프트맥스 함수
ix = np.argmax(p) # 가장 확률이 높은 단어 인덱스
# ix는 예측된 단어의 인덱스 해당 인덱스를 원-핫 벡터로 변환하여
# 다음 시간 스텝의 입력 x로 사용
# 이렇게 매번 예측된 단어를 다음 입력으로 주어
# 모델이 단어 시퀀스를 순차적으로 예측할 수 있도록 한다.
x = np.zeros((vocab_size, 1))
x[ix] = 1
# 리스트에 예측된 단어의 인덱스 저장
ixes.append(ix)
# ixes에 저장된 단어 인덱스들을 실제 단어로 변환한 후,
# 공백으로 구분하여 하나의 문자열로 만든다.
pred_words = ' '.join(ix_to_word[i] for i in ixes)
return pred_words학습 루프
모든 준비가 끝났으니 한번 사용해보겠습니다.
# 학습 파라미터
epochs = 10000
h_size = 100
seq_len = 3
learning_rate = 1e-2아래 코드에 대한 이해를 돕기위해 추가로 작성하자면 inputs가 ["나라의", "말이", "중국과"]라면 targets는 [''말이", "중국과", "달라"] 이렇게 구성되어 targets는 inputs의 다음 단어들이다.
data = """
나라의 말이 중국과 달라
문자와 서로 통하지 아니하니,
이런 까닭으로 어리석은 백성이 이르고자 할 바가 있어도
마침내 제 뜻을 능히 펴지 못할 사람이 많다.
내가 이를 위하여 가엾이 여겨
새로 스물여덟 자를 만드노니
사람마다 하여금 쉬이 익혀 날마다 쓰는 데 편하게 하고자 할 따름이다.
"""
tokens, vocab_size, word_to_ix, ix_to_word = data_preprocessing(data)
U, W, V = init_weights(h_size, vocab_size)
p = 0
hprev = np.zeros((h_size,1))
for epoch in range(epochs):
for p in range(len(tokens) - seq_len):
inputs = [word_to_ix[tok] for tok in tokens[p:p + seq_len]]
targets = [word_to_ix[tok] for tok in tokens[p + 1:p + seq_len + 1]]
# 순전파
loss, ps, hs, xs = feedforward(inputs, targets, hprev)
# 역전파
dU, dW, dV, hprev = backward(ps, hs, xs)
# 가중치 업데이트
W -= learning_rate * dW
U -= learning_rate * dU
V -= learning_rate * dV
# 100 에포크마다 현재 손실값 출력
if epoch%100 == 0:
print(f'epoch {epoch}, loss: {loss}')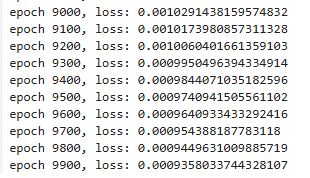
손실 값은 다음과 같이 나왔고 아래 코드를 통해 결과를 확인해보겠다.
while 1:
try:
user_input = input("input: ")
if user_input == 'break':
break
response = predict(user_input,40)
print(response)
except:
print('up on try again!')"나라의"를 입력한 경우

"중국과"를 입력한 경우

아무래도 바닐라 RNN이라서 성능이 아쉬운 것 같다. 재밌는 실습이였다.
'논문' 카테고리의 다른 글
| LSTM 구현 (1) | 2024.12.17 |
|---|---|
| Attention Is All You Need (0) | 2024.12.10 |
| Transformer (1) | 2024.12.04 |
| Seq2seq+Attention (0) | 2024.11.25 |
| Seq2seq (0) | 2024.11.25 |




