AI 전문가가 되고싶은 사람
LSTM 구현 본문
https://www.youtube.com/watch?v=nvJz9maIIRE&t=121s
훈민정음 문장을 학습시켜 한 구절을 입력했을 때 이후 구절을 출력하도록 LSTM 모델을 실습해 보았다. 이전에 다뤘던 RNN에 비해 구조가 더 복잡하여 이해하는 데 시간이 더 걸렸지만, 정확히 기록해 두어 잊지 않도록 해야겠다.
LSTM 구현 순서
1. 데이터 전처리
2. 활성화 함수 구현
3. LSTM 클래스 정의 ( 초기화, 상태 초기화, 순전파, 역전파, 학습, 테스트 )
4. 학습 및 평가
데이터 전처리
이전 글인 RNN과 같이 사용 문장은 다음과 같다.
사용 문장
나라의 말이 중국과 달라 문자와 서로 통하지 아니하니, 이런 까닭으로 어리석은 백성이 이르고자 할 바가 있어도 마침내 제 뜻을 능히 펴지 못할 사람이 많다. 내가 이를 위하여 가엾이 여겨 새로 스물여덟 자를 만드노니 사람마다 하여금 쉬이 익혀 날마다 쓰는 데 편하게 하고자 할 따름이다.
def data_preprocessing(data):
data = re.sub('[^가-힣]', ' ', data) # 한글 이외의 문자 제거
tokens = data.split() # 단어 단위로 분리
vocab = list(set(tokens)) # 고유 단어 집합
vocab_size = len(vocab) # 단어 집합의 크기
word_to_ix = {word: i for i, word in enumerate(vocab)} # 단어 -> 인덱스
ix_to_word = {i: word for i, word in enumerate(vocab)} # 인덱스 -> 단어
return tokens, vocab_size, word_to_ix, ix_to_word
활성화 함수 구현
LSTM의 작동 원리를 나타내는 그림에서 Sigmoid, Tanh, 그리고 Softmax 함수가 각각의 역할에 따라 사용되고 있다는 것을 알 수 있다.
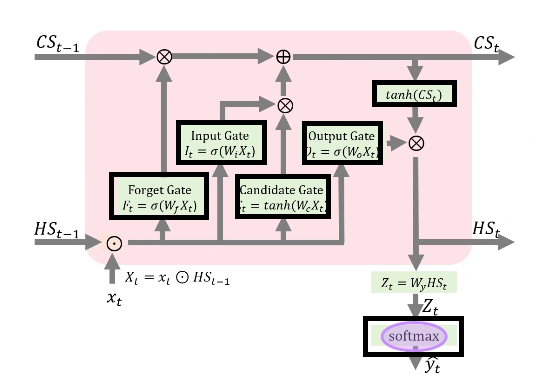
아래와 같이 활성화 함수를 구현하였다.
# 활성화 함수
def sigmoid(input):
return 1 / (1 + np.exp(-input))
def sigmoid_derivative(input):
return input * (1-input)
def tanh(input, derivative=False):
return np.tanh(input)
def tanh_derivative(input):
return 1 - input**2
def softmax(input):
return np.exp(input) / np.sum(np.exp(input))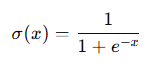
Sigmoid 함수의 경우 Forget Gate, Input Gate, Output Gate의 활성화 함수로 사용된다. 또한, 역전파 과정에서 필요한 그래디언트(기울기)를 계산하는 데 사용하는 도함수 또한 정의하였다.
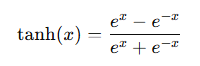
다음으로 tanh 함수는 Candidate Gate 계산에서 사용된다. 마찬가지로 도함수를 정의하였다.

Softmax는 최종 출력 단계에서 사용되며, 각 단어가 특정 클래스에 속할 확률을 계산한다.
LSTM 클래스 정의
class LSTM:
def __init__(self, input_size, hidden_size, output_size, num_epochs, learning_rate):
# Hyperparameters
self.learning_rate = learning_rate
self.hidden_size = hidden_size
self.num_epochs = num_epochs
# Forget Gate
# 이전 셀 상태 중 유지할 정보와 버릴 정보 결정
self.Wf = np.random.randn(hidden_size, input_size)*0.1
self.bf = np.zeros((hidden_size, 1))
# Input Gate
# 새로운 정보를 셀 상태에 얼마나 추가할지 결정
self.Wi = np.random.randn(hidden_size, input_size)*0.1
self.bi = np.zeros((hidden_size, 1))
# Candidate Gate
# 새로운 정보를 생성
self.Wc = np.random.randn(hidden_size, input_size)*0.1
self.bc = np.zeros((hidden_size, 1))
# Output Gate
# 출력값 결정
self.Wo = np.random.randn(hidden_size, input_size)*0.1
self.bo = np.zeros((hidden_size, 1))
# Final Gate
# LSTM의 최종 출력값을 계산
self.Wy = np.random.randn(output_size, hidden_size)
self.by = np.zeros((output_size, 1))위 코드는 LSTM 모델의 초기화 부분으로, 각 게이트와 출력층에 필요한 파라미터들을 정의하고 초기화한다.
LSTM은 각 타임스텝에서 입력과 이전 은닉 상태를 사용하여 게이트를 통해 정보를 처리하기에 이 초기화 코드는 학습 가능한 모든 파라미터를 정의하고, 학습 중 데이터와 손실 함수에 의해 점진적으로 업데이트 된다.
# 네트워크 메모리 리셋
def reset(self):
# 입력값 저장 (각 타임스텝 값이 저장된다.)
self.X = {}
# 각 타임스텝의 은닉 상태 저장
# 초기 은닉 상태는 모든 값이 0인 벡터로 설정된다.
self.HS = {-1: np.zeros((self.hidden_size, 1))}
# 각 타임스텝의 셀 상태를 저장
# 초기 셀 상태도 은닉 상태와 마찬가지로 0으로 설정된다.
self.CS = {-1: np.zeros((self.hidden_size, 1))}
# Candidate 상태 저장
self.C = {}
# Output Gate 저장
self.O = {}
# Forget Gate 저장
self.F = {}
# Input Gate 저장
self.I = {}
# 출력값 저장
self.outputs = {}LSTM 네트워크의 메모리를 초기화하는 메서드로, 학습이나 예측을 시작할 때 상태를 리셋하여 새로운 시퀀스 데이터를 처리할 준비를 한다. LSTM은 이전 타임스텝의 은닉 상태와 셀 상태를 계속 참조하기에, 새로운 데이터나 시퀀스를 처리하기 전 반드시 이러한 상태를 초기화해야한다.
* 초기화하는 이유
LSTM 네트워크는 시퀀스 데이터를 처리할 때 시간축 상의 상태 전이를 활용하기에 새로운 시퀀스가 시작될 때 이전 데이터의 잔여 상태가 남아 있다면 결과가 왜곡될 수 있다.
순전파
# Forward 순전파
def forward(self, inputs):
# self.reset()
x = {}
outputs = []
# inputs는 단어 ID로 구성된 시퀀스는 [1,3,5]와 같은 데이터가 들어온다.
for t in range(len(inputs)):
x[t] = np.zeros((vocab_size , 1))
x[t][inputs[t]] = 1
# 현재 입력 x[t]와 이전 시점의 은닉 상태 HS[t-1]를 연결하여 새로운 입력 벡터 X[t] 생성
self.X[t] = np.concatenate((self.HS[t - 1], x[t]))
# 어떤 정보를 잊을지 결정
self.F[t] = sigmoid(np.dot(self.Wf, self.X[t]) + self.bf)
# 어떤 정보를 새롭게 기억할지 결정
self.I[t] = sigmoid(np.dot(self.Wi, self.X[t]) + self.bi)
# 입력 게이트에 의해 선택될 후보 셀 상태 계산
self.C[t] = tanh(np.dot(self.Wc, self.X[t]) + self.bc)
# 최종 출력 h[t]에서 어떤 정보를 출력할지 결정
self.O[t] = sigmoid(np.dot(self.Wo, self.X[t]) + self.bo)
# 현재 셀 상태는 Forget Gate와 Input Gate의 영향을 받아 갱신
self.CS[t] = self.F[t] * self.CS[t - 1] + self.I[t] * self.C[t]
# Output Gate와 셀 상태의 활성화를 기반으로 은닉 상태 결정
self.HS[t] = self.O[t] * tanh(self.CS[t])
# 각 시점 t에서 은닉 상태 HS[t]를 사용해 최종 출력값 계산
outputs += [np.dot(self.Wy, self.HS[t]) + self.by]
return outputs역전파
# 역전파
def backward(self, errors, inputs):
# 가중치 및 편향의 그래디언트를 모두 초기화한다.
dLdWf, dLdbf = 0, 0
dLdWi, dLdbi = 0, 0
dLdWc, dLdbc = 0, 0
dLdWo, dLdbo = 0, 0
dLdWy, dLdby = 0, 0
# 다음 타임스텝으로 전달될 오류를 초기화한다.
dh_next, dc_next = np.zeros_like(self.HS[0]), np.zeros_like(self.CS[0])
# RNN과 마찬가지로 입력의 타임스텝을 거꾸로 순회하며,
# 각 타임스텝에서 오차를 기반으로 가중치와 편향의 그래디언트를 계산한다.
for t in reversed(range(len(inputs))):
error = errors[t]
# 출력 가중치와 출력 편향의 그래디언트를 계산한다.
dLdWy += np.dot(error, self.HS[t].T) #𝜕𝐿/𝜕𝑊𝑦
dLdby += error #𝜕𝐿/𝜕b𝑦 = (𝜕𝐿/𝜕z_t)(𝜕z_t/𝜕b𝑦) = error x 1 (Zt = WyHSt + by)
# 출력 레이어로부터 전달된 오차와
# 다음 타임스텝의 오차를 더하여 Hidden State의 총 그래디언트를 계산한다.
# Hidden State Error
dLdHS = np.dot(self.Wy.T, error) + dh_next #𝜕𝐿/𝜕𝐻𝑆
# Output Gate Weights and Biases Errors
# Hidden State의 오차(dLdHS)와 Cell State의 tanh 결과(tanh(self.CS[t]))를 곱한 후,
# Output Gate의 활성화 함수(sigmoid)의 도함수를 곱한다.
dLdo = tanh(self.CS[t]) * dLdHS * sigmoid_derivative(self.O[t])
# dLdWo와 dLdbo는 Output Gate의 가중치와 편향의 그래디언트이다.
dLdWo += np.dot(dLdo, inputs[t].T)
dLdbo += dLdo
# Cell State Error
# Hidden State의 그래디언트(dLdHS)와 Output Gate의 활성화 결과(self.O[t])
# Cell State의 tanh 도함수를 사용하여 계산한다.
# 이전 타임스텝에서 전달된 Cell State의 그래디언트(dc_next)를 추가한다.
dLdCS = tanh_derivative(tanh(self.CS[t])) * self.O[t] * dLdHS + dc_next
# Forget Gate Weights and Biases Errors
# dLdf는 현재 Cell State의 그래디언트(dLdCS)와 이전 타임스텝의 Cell State(self.CS[t - 1])를 곱하고,
# Forget Gate의 활성화 함수(sigmoid)의 도함수를 곱하여 계산한다.
dLdf = dLdCS * self.CS[t - 1] * sigmoid_derivative(self.F[t])
# dLdWf와 dLdbf는 Forget Gate의 가중치와 편향의 그래디언트이다.
dLdWf += np.dot(dLdf, inputs[t].T)
dLdbf += dLdf
# Input Gate Weights and Biases Errors
# dLdi는 현재 Cell State의 그래디언트(dLdCS)와 Candidate Cell State(self.C[t])를 곱하고,
# Input Gate의 활성화 함수(sigmoid)의 도함수를 곱하여 계산한다.
dLdi = dLdCS * self.C[t] * sigmoid_derivative(self.I[t])
# dLdWi와 dLdbi는 Input Gate의 가중치와 편향의 그래디언트이다.
dLdWi += np.dot(dLdi, inputs[t].T)
dLdbi += dLdi
# Candidate Gate Weights and Biases Errors
# dLdc는 현재 Cell State의 그래디언트(dLdCS)와 Input Gate의 활성화 결과(self.I[t])를 곱하고,
# Candidate Gate의 활성화 함수(tanh)의 도함수를 곱하여 계산한다.
dLdc = dLdCS * self.I[t] * tanh_derivative(self.C[t])
# dLdWc와 dLdbc는 Candidate Gate의 가중치와 편향의 그래디언트이다.
dLdWc += np.dot(dLdc, inputs[t].T)
dLdbc += dLdc
# Concatenated Input Error (Sum of Error at Each Gate!)
# X[t]의 그래디언트를 계산하고, 이를 HS와 CS의 그래디언트로 분리하여 다음 타임스텝으로 전달한다.
d_z = np.dot(self.Wf.T, dLdf) + np.dot(self.Wi.T, dLdi) + np.dot(self.Wc.T, dLdc) + np.dot(self.Wo.T, dLdo)
# Error of Hidden State and Cell State at Next Time Step
dh_next = d_z[:self.hidden_size, :]
dc_next = self.F[t] * dLdCS
for d_ in (dLdWf, dLdbf, dLdWi, dLdbi, dLdWc, dLdbc, dLdWo, dLdbo, dLdWy, dLdby):
# 그래디언트를 -1에서 1 사이로하여 그래디언트 폭주 문제를 방지한다.
np.clip(d_, -1, 1, out=d_)
# 학습률(learning_rate)을 사용하여 그래디언트를 기반으로 가중치 및 편향을 업데이트한다.
self.Wf += dLdWf * self.learning_rate * (-1)
self.bf += dLdbf * self.learning_rate * (-1)
self.Wi += dLdWi * self.learning_rate * (-1)
self.bi += dLdbi * self.learning_rate * (-1)
self.Wc += dLdWc * self.learning_rate * (-1)
self.bc += dLdbc * self.learning_rate * (-1)
self.Wo += dLdWo * self.learning_rate * (-1)
self.bo += dLdbo * self.learning_rate * (-1)
self.Wy += dLdWy * self.learning_rate * (-1)
self.by += dLdby * self.learning_rate * (-1)학습 및 테스트
# Train
def train(self, inputs, labels):
for _ in tqdm(range(self.num_epochs)): # 지정된 epoch 동안 반복
self.reset() # 이전 상태를 초기화
input_idx = [Word_to_ix[input] for input in inputs] # 입력 데이터를 인덱스 형태로 변환
predictions = self.forward(input_idx) # forward 메서드를 통해 예측값 계산
errors = []
for t in range(len(predictions)):
errors += [softmax(predictions[t])] # softmax로 출력값을 확률로 변환
errors[-1][Word_to_ix[labels[t]]] -= 1 # 실제 정답 레이블 위치의 확률을 낮춰 오차 계산
self.backward(errors, self.X) # 역전파로 가중치 업데이트
def test(self, inputs, labels):
accuracy = 0 # 정확도를 추적하는 변수
probabilities = self.forward([Word_to_ix[input] for input in inputs]) # forward 메서드로 출력 계산
gt = ''
output = '나라의 ' # 예측값 출력 초기화
for q in range(len(labels)):
prediction = ix_to_Word[np.argmax(softmax(probabilities[q].reshape(-1)))]
gt += inputs[q] + ' '
output += prediction + ' ' # 예측값 누적
if prediction == labels[q]: # 예측값과 실제값 비교
accuracy += 1
print('실제값: ', gt) # 실제 레이블 출력
print('예측값: ', output) # 예측값 출력결과
hidden_size = 25
# data preparation
tokens, vocab_size, Word_to_ix, ix_to_Word = data_preprocessing(data)
train_X, train_y = tokens[:-1], tokens[1:]
lstm = LSTM(input_size=vocab_size + hidden_size, hidden_size=hidden_size, output_size=vocab_size, num_epochs=1000,
learning_rate=0.05)
##### Training #####
lstm.train(train_X, train_y)
lstm.test(train_X, train_y)
마무리
정확히 모든 부분을 이해했는지 묻는다면, 그렇다고 확신할 수 없다. 일부는 그렇구나 하고 넘어간 부분들이 있어, 이후 복습을 통해 더 깊이 이해하려고 해야겠다.
'논문' 카테고리의 다른 글
| Seq2Seq로 Chatbot 구현 (0) | 2025.01.16 |
|---|---|
| BERT: Pre-training of Deep Bidirectional Transformers forLanguage Understanding (2) | 2024.12.26 |
| Attention Is All You Need (0) | 2024.12.10 |
| RNN 구현 (1) | 2024.12.06 |
| Transformer (1) | 2024.12.04 |




